測量成果である図面に辺長や座標などの数値が記載されており、その数値は観測したデータをコンピューターで計算し算出された数値です。
しかし、その成果である数値は、調節や補正で加工された数値であり、同じ現場でも時期や測量者、またその目的によっては、その測量成果の数値に関して許容の範囲内でそれぞれ相違が生じます。
今回は、どのような要因で測量成果が調整・補正されるのかを記事にしていきたいと思ってます。
今回は、一例をご紹介します。本記事以外にも様々な補正や調節があるので、きちんとした情報を知りたい方は、測量に関する書籍や国土地理院の作業規定準則を参考にして頂ければと思います。
真値と最確値とは
測量技術者ではない方は、図面等に記載のある座標値や辺長は、絶対に変わらない数値である真値(真実の数値)だと思ってしまいます。
しかし、この図面などに記載された成果の値は、現地で測った距離と角度のデータを元に、測量で生じる誤差を調節したり、また補正し算出された数値であり、最も確からしい数値である最確値と呼ばれるものになります。
私たちが手にする測量成果はあくまで、最確値(最も確からしい数値)であり、真値(神のみぞ知る真実の数値)ではありません。
実際に測ってきた3次元の観測記録を、平面の2次元の情報にする。
実際に現場で測量した測量記録は、距離と角度に関する情報です。
その距離と角度に関する情報は3次元の情報であり、それを私たちが理解しやすいように平面である2次元にする計算を行います。
この3次元の観測記録を2次元の平面の数値にする上で、測量機器の目盛り誤差の調節や、また地球という球体を平面上に表現するための補正など、様々な調節や補正を行います。
測量の誤差について
現在の測量機器は精度がとても高く、距離は1ミリ単位で角度は1秒単位の高精度で測ることが出来ます。
上記ほどの精度で測るためには、人間にはどうしようもない測量機械の傾きによる誤差、測量機械が持っている目盛りの誤差、そして気温などを考慮しなければなりません。
以上のような誤差等を考慮をして、出来るだけ正しい値にするための作業が、測量技術者の仕事になります。
この誤差の調節などにより、同じ現場でも時期や測量者、またその調節方法などによって、許容の範囲内で測量の誤差が生じます。
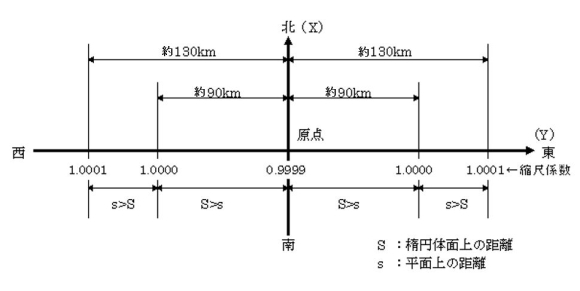
球面から平面に補正する縮尺係数
縮尺係数とは、球体である地球を、私たちが理解し易い平面に投影をする際に、一定の誤差の範囲内に収めるために調節する係数です。
この球面を平面に投影する作業は、日本では主に平面直角座標系が使用されており、一つの座標系の誤差が1万分の1の範囲内に収まるようになってます。
これは、土地を測量する際に、10mで1mmほど補正されることになります。
原点では1mm短くなり、原点から130キロ離れている場合は1mm長いことになり、また原点から90キロ離れている場合は補正は必要ありません。(図1を参照)
平面直角座標系は不動産登記法でも平成16年度から採用されてますが、それ以前に測量した場合や、近くにその基準となる点がないなどの様々な要因で、平面直角座標系が使用することが出来ない場合があります。
そのため、測量成果として図面を手にした時は、平面直角座標系で作成されているかを確認することが、図面を見る際に大切なことになります。
平面直角座標系で作成されている場合は、世界測地系(測地成果2011等)の記載がされています。
2011年は東日本大震災があり、それによる地形の移動等を考慮した成果であるとの意味です。
ただ、1ミリは、実際に測る際に機械によって異なることがありますし、また現地も工事などにより地物や地形が移動していることも考えれば、それを心配する必要はありません。
球体を平面に投影する
以下の図のように、平面直角座標系は、球面である地球を平面に投影するために、原点からの距離に応じて縮尺係数で調節します。
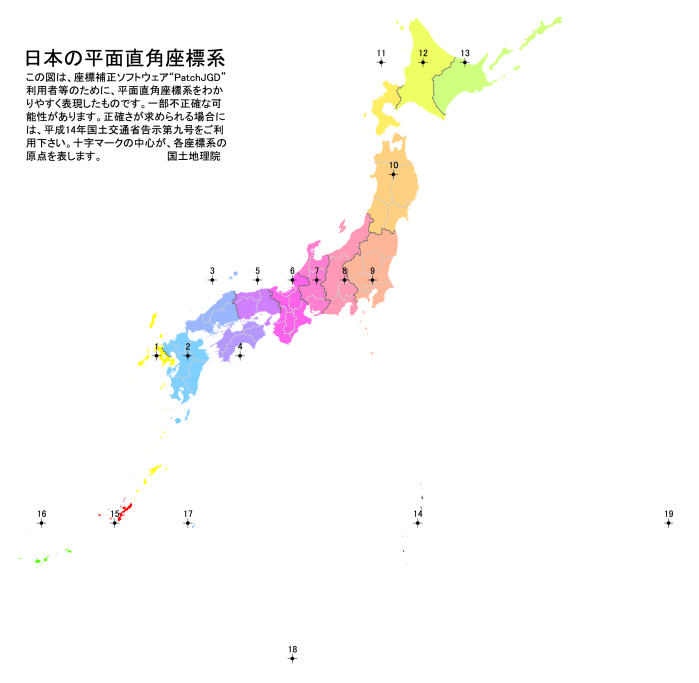
球体を平面に投影するために全国を19の座標系に分ける
球体を平面に投影した際に、その誤差を1万分の1の範囲に収めるために、日本全国19の座標系に分けます。
まとめ
最後まで読んで下さりありがとうございました。
専門家が図った数値だから、その数値は何回測量しても同じと考えてしまいますが、その測量成果は同じ現場であっても測量ごとに微妙に異なってきます。
土地家屋調査士などの測量技術者は、その相違や誤差等を考慮しなければなりません。
既存の測量成果のデータと、測量して実際に得られた生の観測記録を必ず分けて、測量技術者としての答えを見つけます。
そして、生の観測記録は、調節などの計算であるやめ、測量技術者は必ず何か疑念などがあった時は、必ず現地で測った生の観測記録である距離と角度までさかのぼり、解決の糸口を見つけます。
測量技術者は、ただ測ったりその計算をすることだけでなく、色々な要因で考慮しなければならない、調節や補正を行い、最も正しいと思われる数値である最確値を求めるために、日々努力しています。